【STM32】DSP数字信号处理函数库

发表于 更新于 分类于 本文字数： 1.6k 阅读时长 ≈ 1 分钟
本文介绍了基于ARM Cortex-M处理器的嵌入式系统设计的数字信号处理库CMSIS-DSP，并给出常用的数学运算与信号分析等函数的调用方法。

前言

什么是CMSIS-DSP库？

在ARM的单片机开发中，常用到CMSIS提供的DSP数字信号处理函数库。它为低功耗、高效能嵌入式系统设计，包含了常用的数学和信号处理功能，旨在提高单片机执行DSP算法的效率。它常见的功能模块包括快速数学运算、矩阵运算、滤波器设计、傅里叶变换、插值函数等，涵盖了大多数工程应用中的算法。

DSP库下载与使用

  1. 按照标准流程新建一个STM32CUBEMX工程，生成MDK-ARM版本的代码工程文件。

  2. 在Keil 5中打开Pack Installer，在右侧Pack列表中找到ARM::CMSIS-DSP点击Install，等待安装完毕，出现Up to date即可。

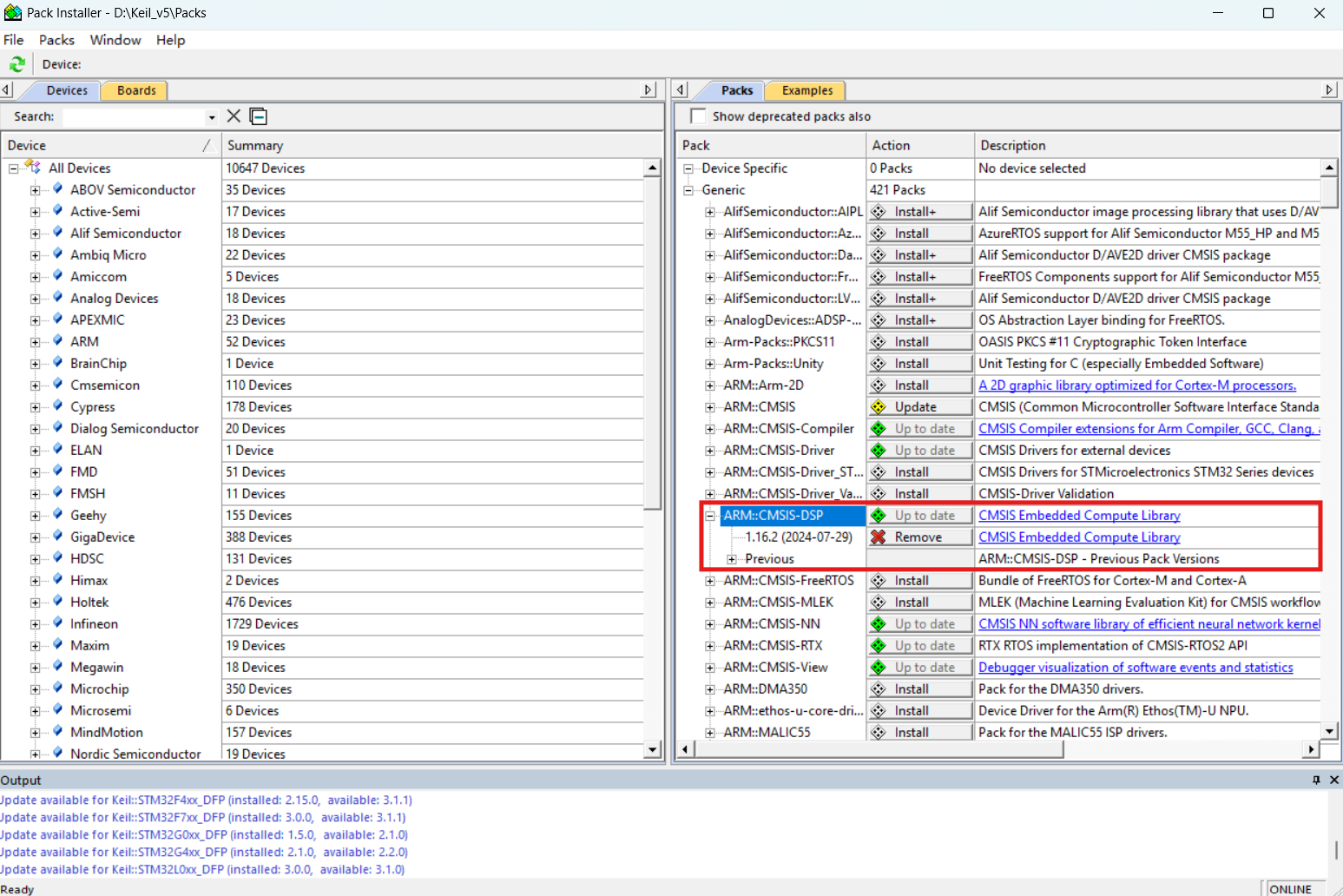
    DSP库安装

  3. 关闭Pack Installer，打开Manage Run-Time Environment，勾选CMSIS目录下的DSP栏，点击OK即可。

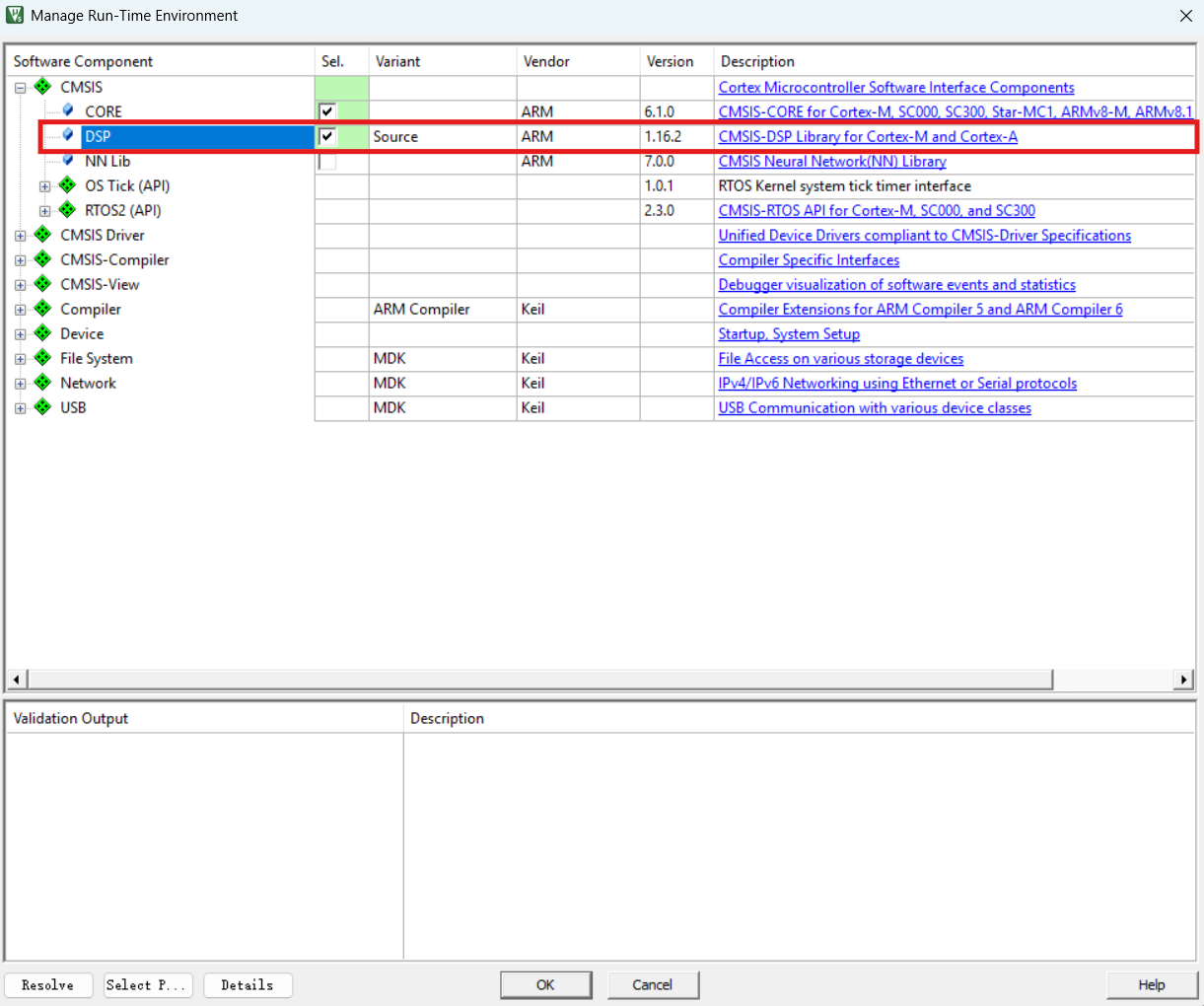
    DSP库使用

  4. 最后在需要使用DSP的头文件中加一行#include "arm_math.h"，即可调用DSP库中的函数了。

基本数学运算

首先解释一下浮点数和定点数的概念

计算机中有两种常见方式存储和处理小数，分别是浮点数和定点数，两种表示方式各有优缺点。（注：“点”即小数点，可从字面意思理解）

浮点数

浮点数表示小数类似科学记数法，它由三个部分组成：符号位、指数部分和尾数部分。

  • 符号位：1位，表示数值的符号。0表示正数，1表示负数。
  • 指数：用于表示数值的大小范围，指数越大，则小数的绝对值越大。
  • 尾数：有效数字部分，尾数越长则数值越精确。

根据IEEE 754标准，单精度浮点数（32位）的结构为1位符号位+8位指数位+23位尾数位，

双精度浮点数（64位）的结构为1位符号位+11位指数位+52位尾数位

例子：数值\(6.25_{(10)}=110.01_{(2)}=1.1001_{(2)}\times2^{10_{(2)}}\)，因此6.25在计算机中使用单精度浮点数表示为\(0 | 00000010 | 000...0011001\)

总结：浮点数能表示非常大范围的数，支持科学记数法，且能提供较高精度，但缺点是对硬件支持要求高，计算耗时较长，且对于某些十进制小数只能近似表示。

定点数

定点数是一种相对简单的数值表示方式，它将小数固定在特定位置，计算时没有浮动的指数部分。定点数通常由两部分组成：整数部分和小数部分，两者的长度是固定的。

定点数通过指定小数位数（Q格式）来决定小数部分的精度，常见的格式有

  • Q15格式：包含1个符号位和15个小数位，剩余位为整数位。其精度为\(1/2^{15}\approx0.00003\)，因此能表示的数值范围为\(-1\)到\(0.99997\)，例如Q15格式中\(32768\)表示\(-1\)，\(32767\)表示\(0.99997\)，\(16384\)表示\(0.5\).
  • Q31格式：包含1个符号位和31个小数位。其精度为\(1/2^{31}\)，因此能表示的数值范围为\(-1\)到\(1-2^{-31}\).

CMSIS-DSP库中Q15格式对应变量类型q15_t，Q31格式对应变量类型q31_t.

【注意事项】

  1. 使用Q15进行定点数运算时，需要确保该数在合法范围\(-32768\)到\(32767\)之间，若超出范围会被截断成\(0x7FFF\)或\(0x8000\). 同理使用Q31类型需确保该数在\(-2147483648\)到\(2147483647\)之间。
  2. 只有同类型的定点数可以运算。两个Q15类型的定点数相乘时，乘积会超出Q15的表示范围，因此需将结果右移15位。同理两个Q31类型的定点数相乘时，结果需右移31位。

总结：定点数能表示的数的范围远小于浮点数，而且由于把小数当作整数进行运算，会损失一定的精度，但是定点数运算能节省大量的时间和空间开销，非常适用于嵌入式系统追求高实时性和低功耗的应用场景。